九点円の定理 思考力を鍛える数学
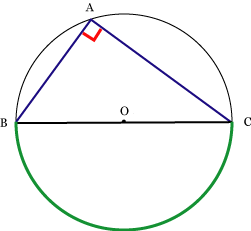
中学3年生 数学 円の性質の利用 練習問題プリント 円と接線において成り立つ定理について理解し、その性質を活用する練習を行なう問題プリントです。T2：円の接線にはどんな性質がありましたか。 s2：接点を通る半径に垂直です。 s3：弦が直径なので，タレスの定理が使えそうです。 ・「円の弦と，その一端を通る接線のつくる角とその角内にある弧に対する円周角」と表現できることを確認する。
円 定理
円 定理- 与えられた方程式が円を表すかどうか，例題を通して考えてみましょう． 問 次の方程式は円を表すか． ( 1 1) x2 y2 = 4 x 2 y 2 = 4 ( 2 2) x2 y2 = 0 x 2 y 2 = 0 ( 3 3) x2 y2 = −3 x 2 y 2 = − 3 →solution ( 1 1 )は円を表す． ( 2 2 )は原点を表す． ( 3 3 )が表す図形は存在 外接円の半径の公式 公式①正弦定理から求める 公式②3 辺と面積から求める 外接円の半径の求め方例題 外接円の性質 性質①外心（外接円の中心）と垂直二等分線 性質②外心と各頂点との距離 外接円の書き方 外接円の練習問題
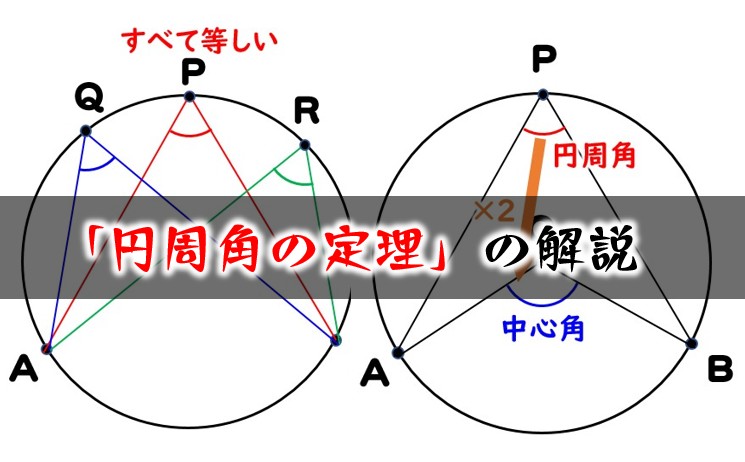
円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
円周上の点 P の座標を (x , y) とおくと，ピタゴラスの定理 そもそも円の直径や座標が簡単に算出できる元はこの円の方程式があるからだと思い、基本に立ち返って勉強しました。たいへん参考になり円の不思議さはまだまだ隠されていると思う。 そして、この試みはジオジェブラの使い方の一つの例になるのではないかと思っている。 円の不思議 （円についてのいろいろな定理） ・・・多角形と円の関係・ミケルの定理・スタイナー点・高田の定理 外接円Oの半径は、正弦定理を用いて、 7√3÷sin60°=7 であるとわかります。（今回は正弦定理の解説ではないので詳しい説明は省きます。） このとき、円周角の定理より、∠APB=60°であることがわかります。 いま、 2PA=3PBになるときのPAの長さ を求めたいので、
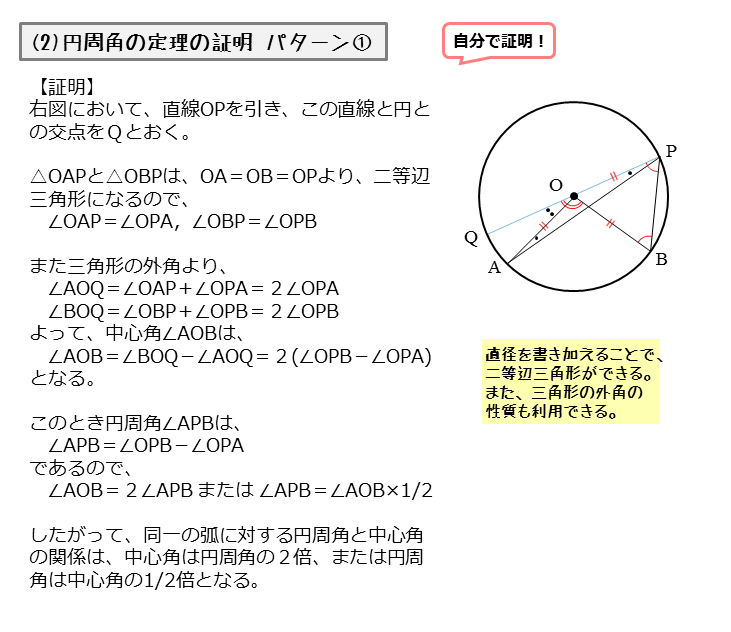
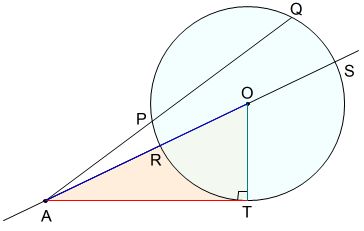
方 べきの 定理とは， 平行でない 2 本の直線と円とが交わって（接して）できる図形の辺の長さの関係 を示している公式です。基本的には 3 つの形があります。 どれも三角形の相似から証明することができます。 ① 2 つの直線の交点が円の内部にあるとき このとき， が成り立ちます。 九点円の定理とは 九点円の定理とは，三角形と円に関する非常に美しい定理です．受験等に役立つことはほとんどないと思いますが，この定理の美しさを鑑賞する価値は十分あります．ぜひ，秩序だった様を存分に味わってください． 九点円の定理： $ abc$ について，以下の $9$ つ 数学Ⅰ1数と式 展開公式・因数分解公式α 絶対値の性質・方程式・不等式 平方根の性質・2重根号22次方程式・2次関数 平方完成 2次方程式の解・重解・解の個数 関数の平行移動・対称移動3図形と計量 正弦定理・余弦定理 $90^{ \
円 定理のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
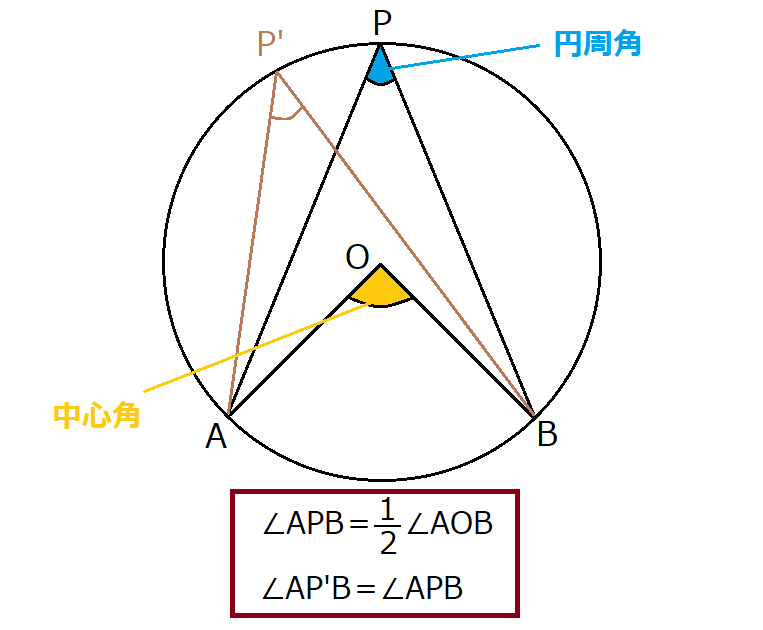
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 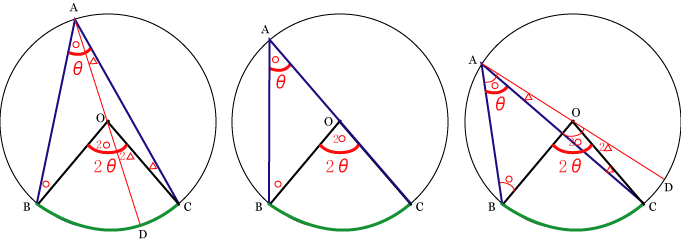 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 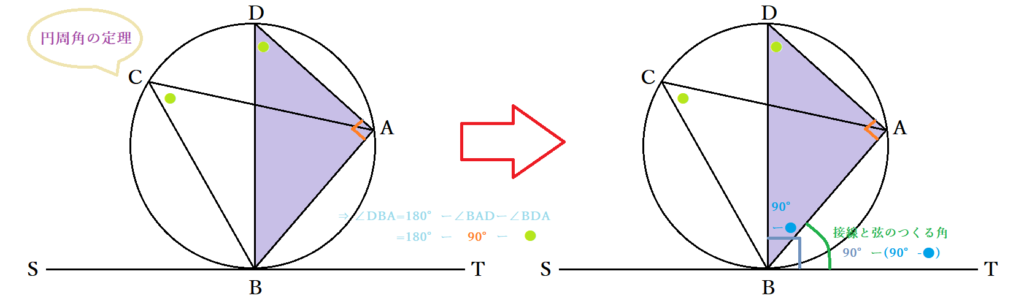 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 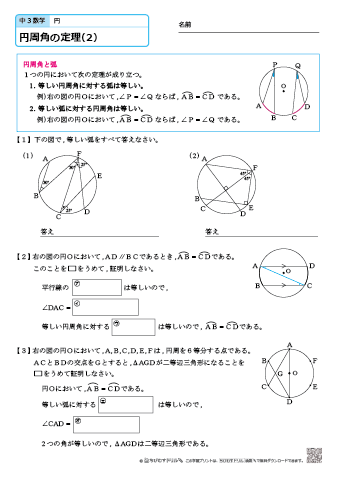 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 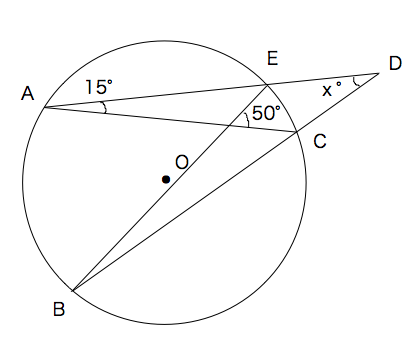 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 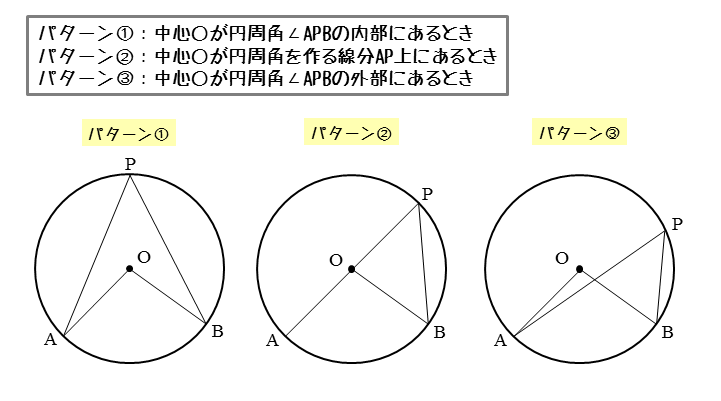 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 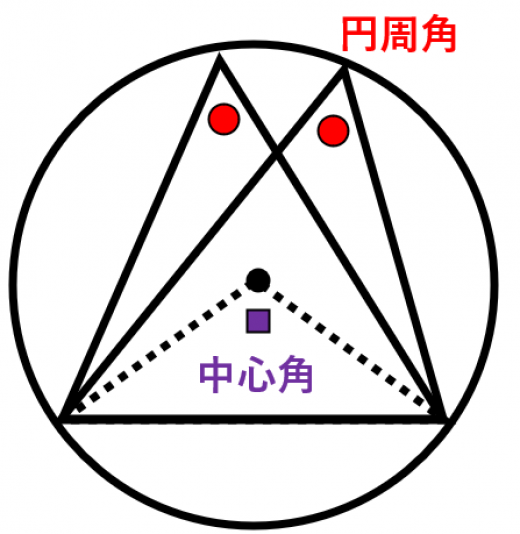 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 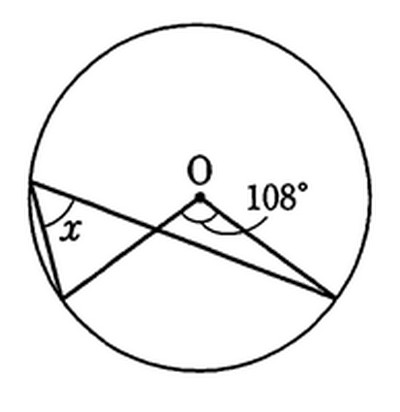 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
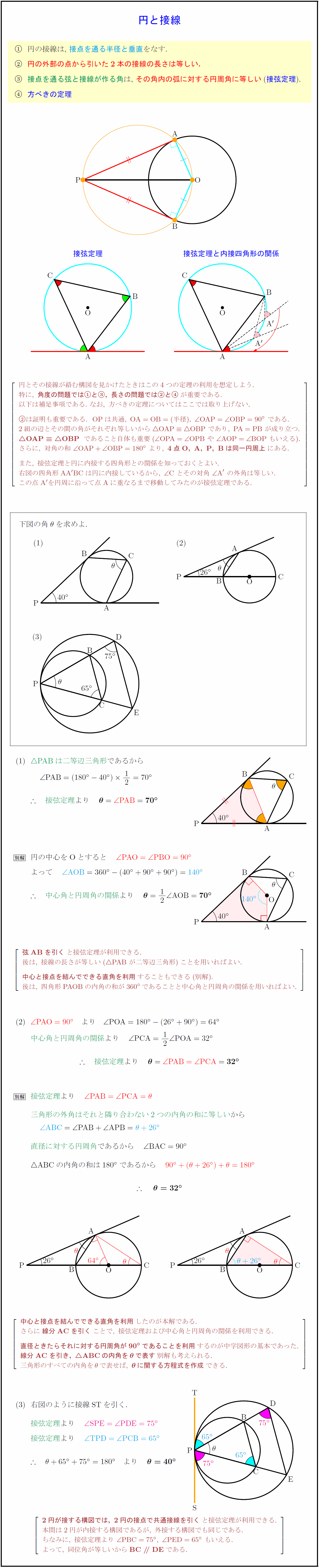 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 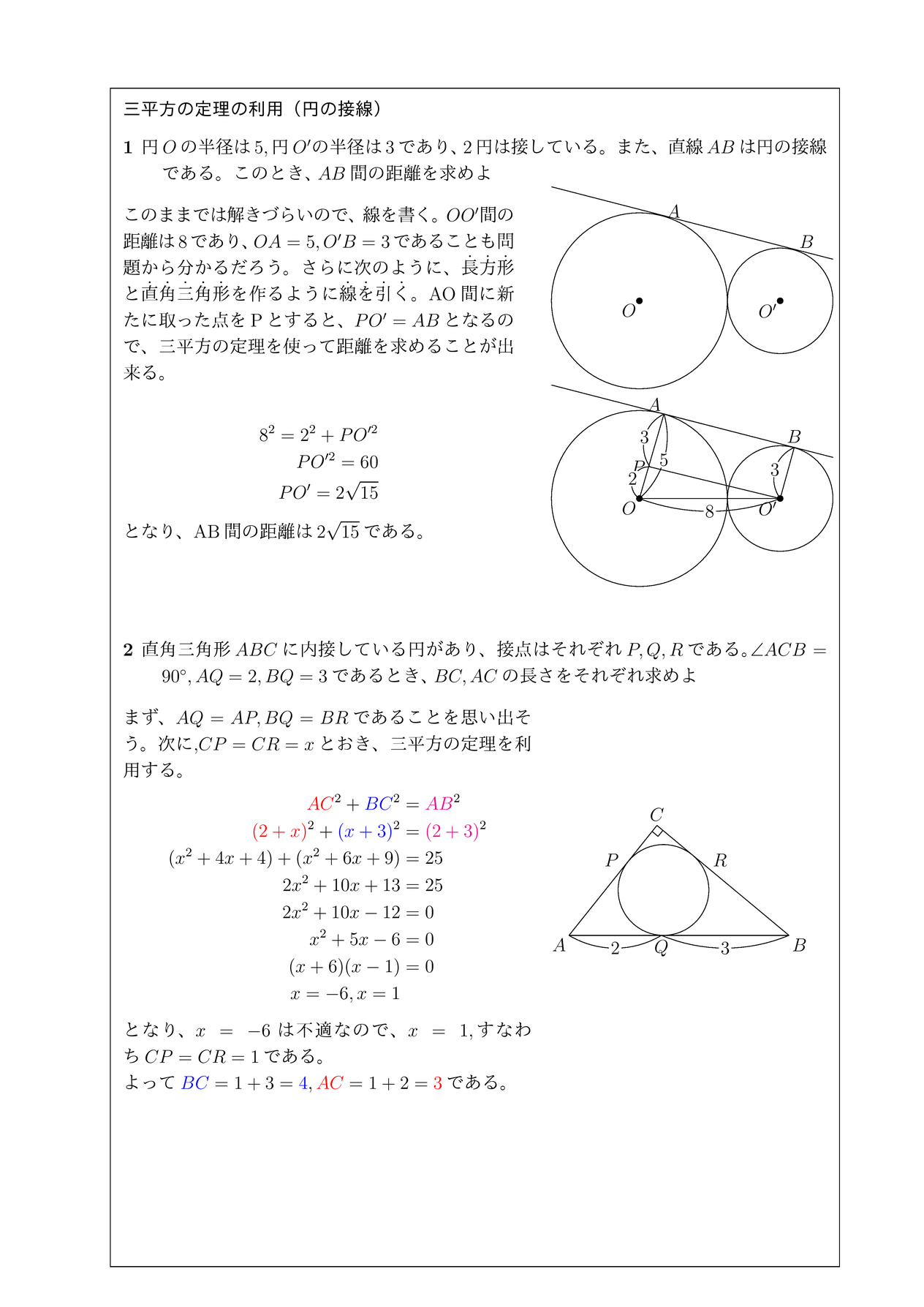 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 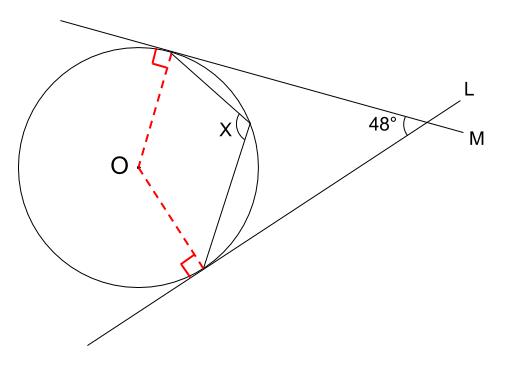 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 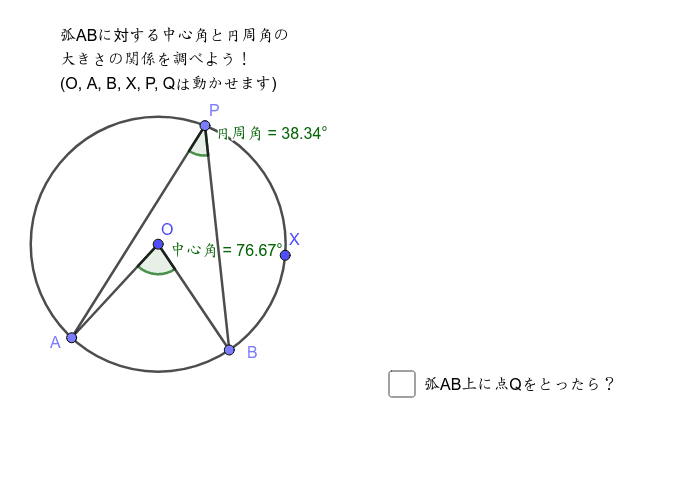 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 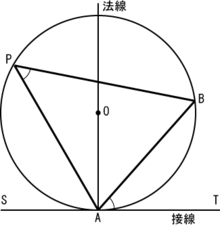 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 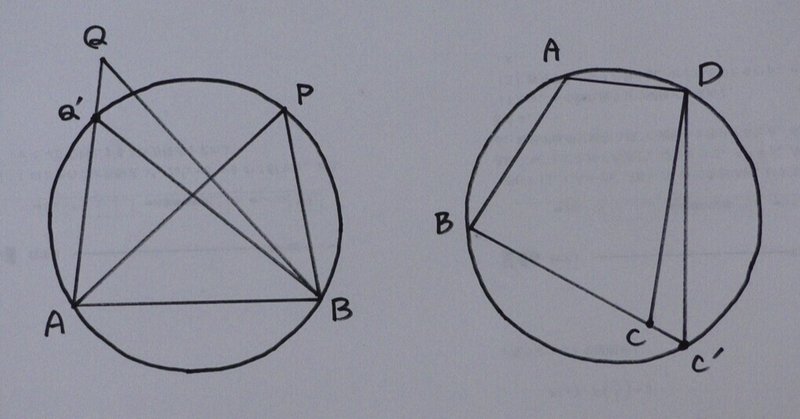 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
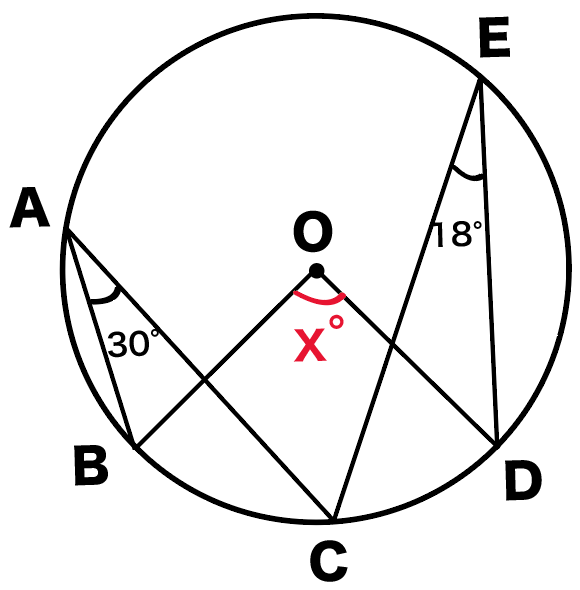 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 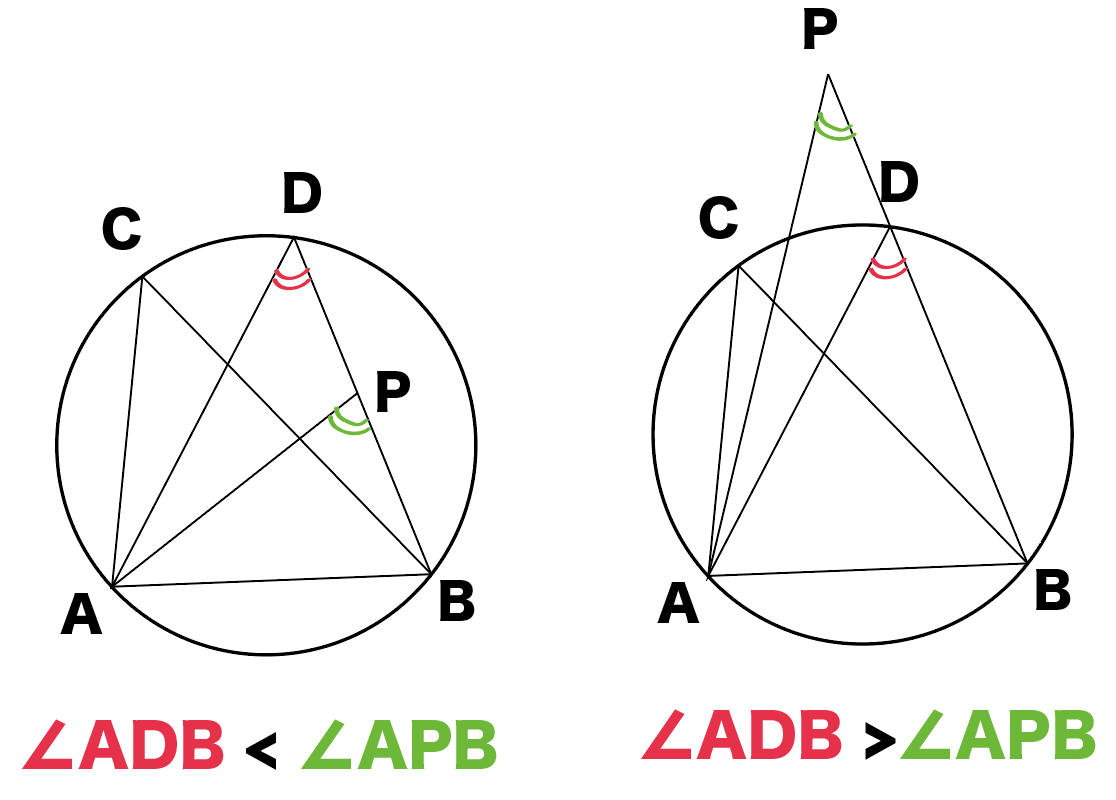 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
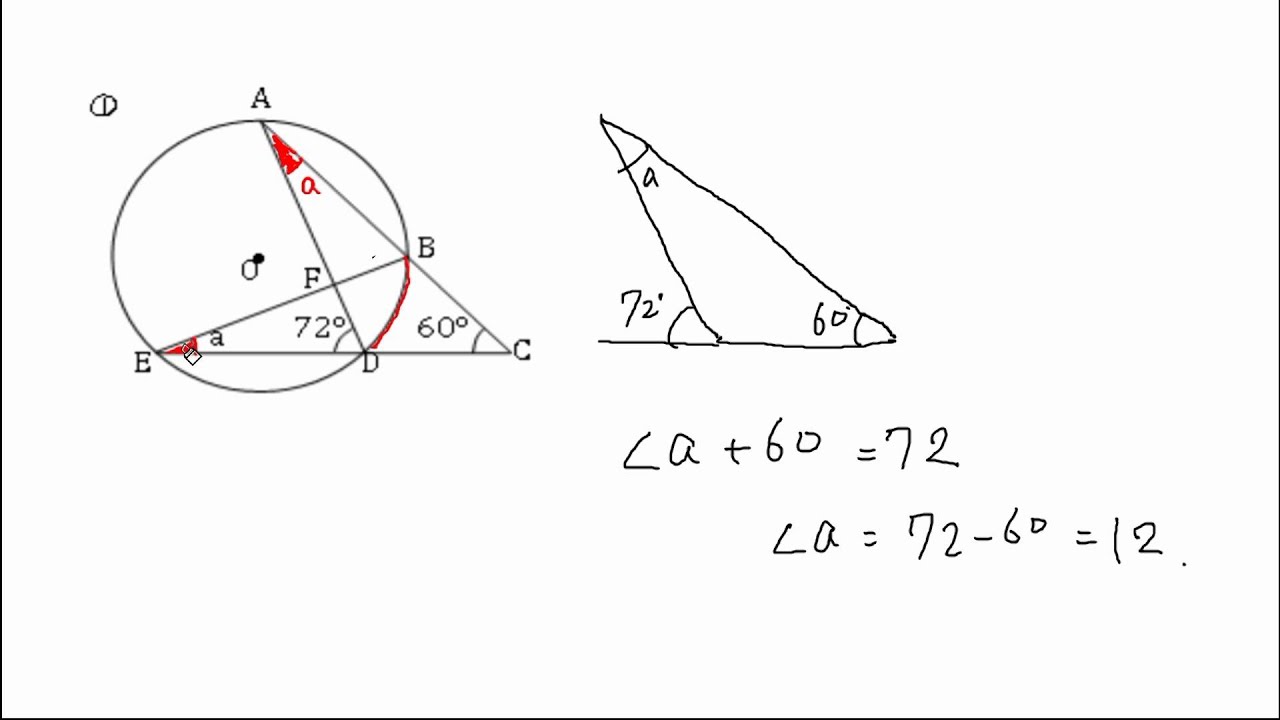 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 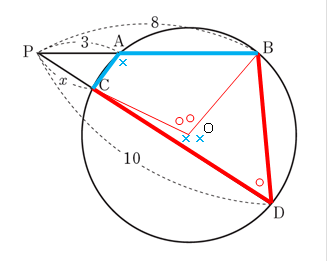 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
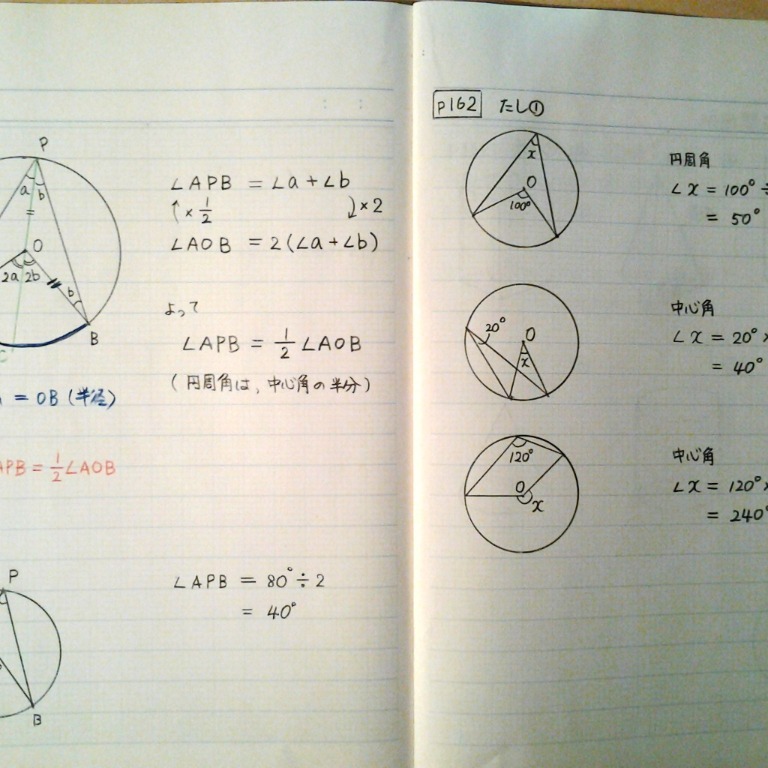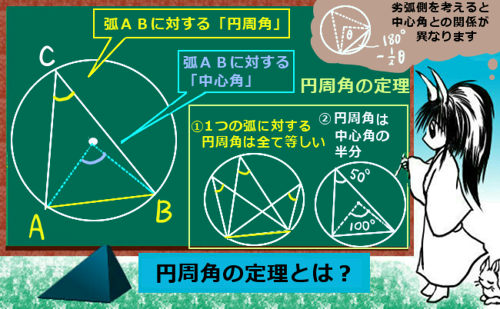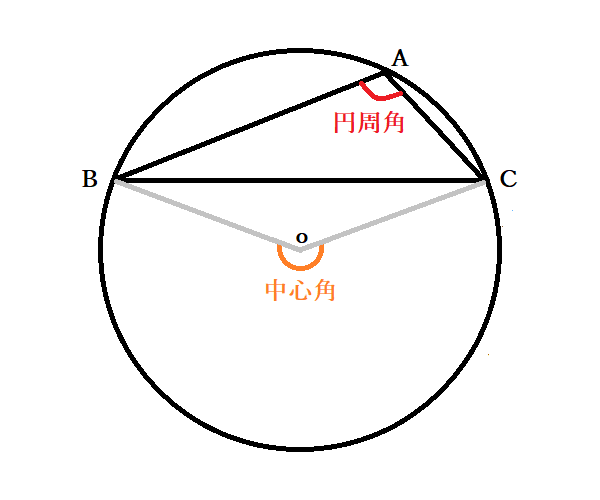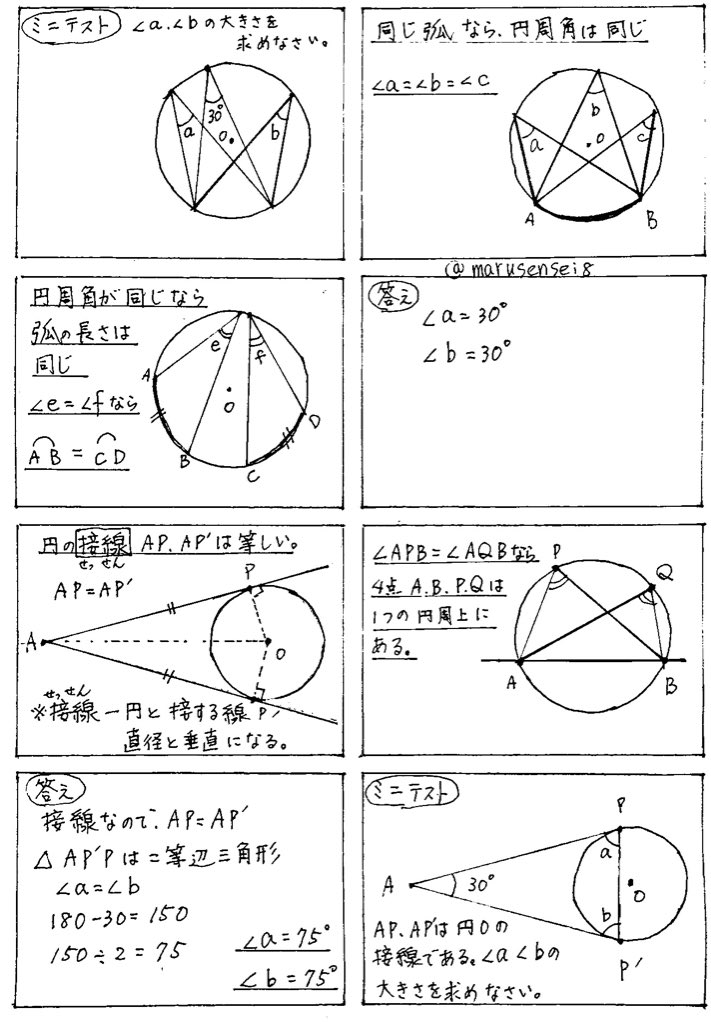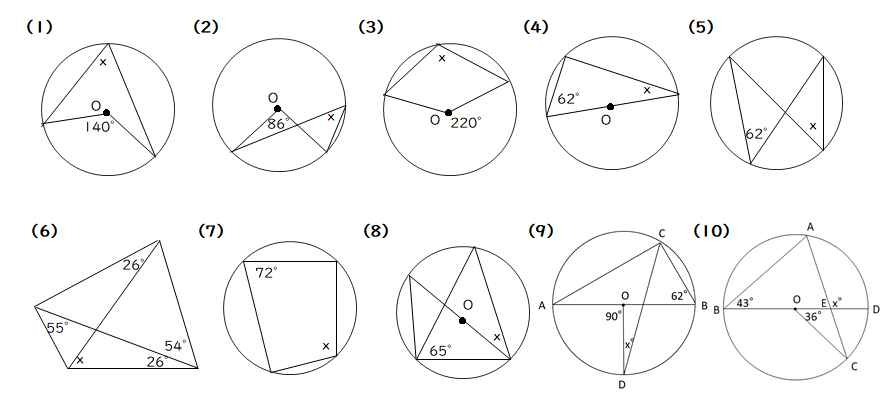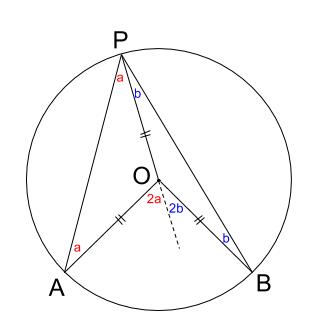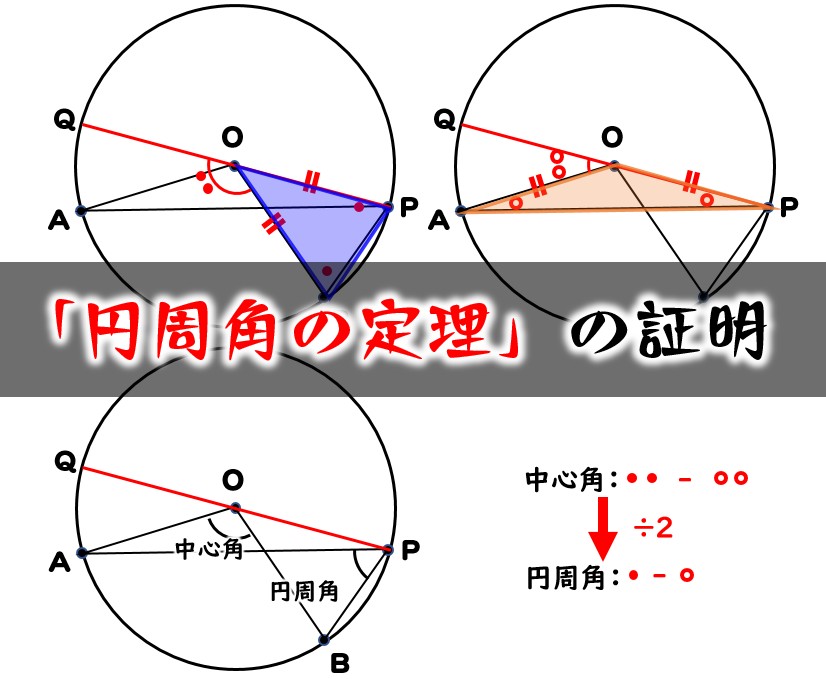 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 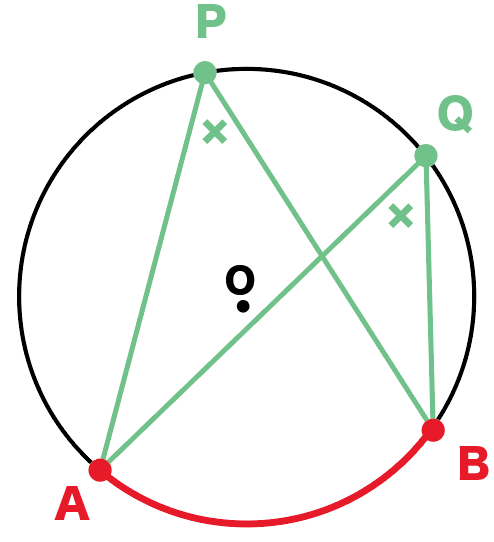 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 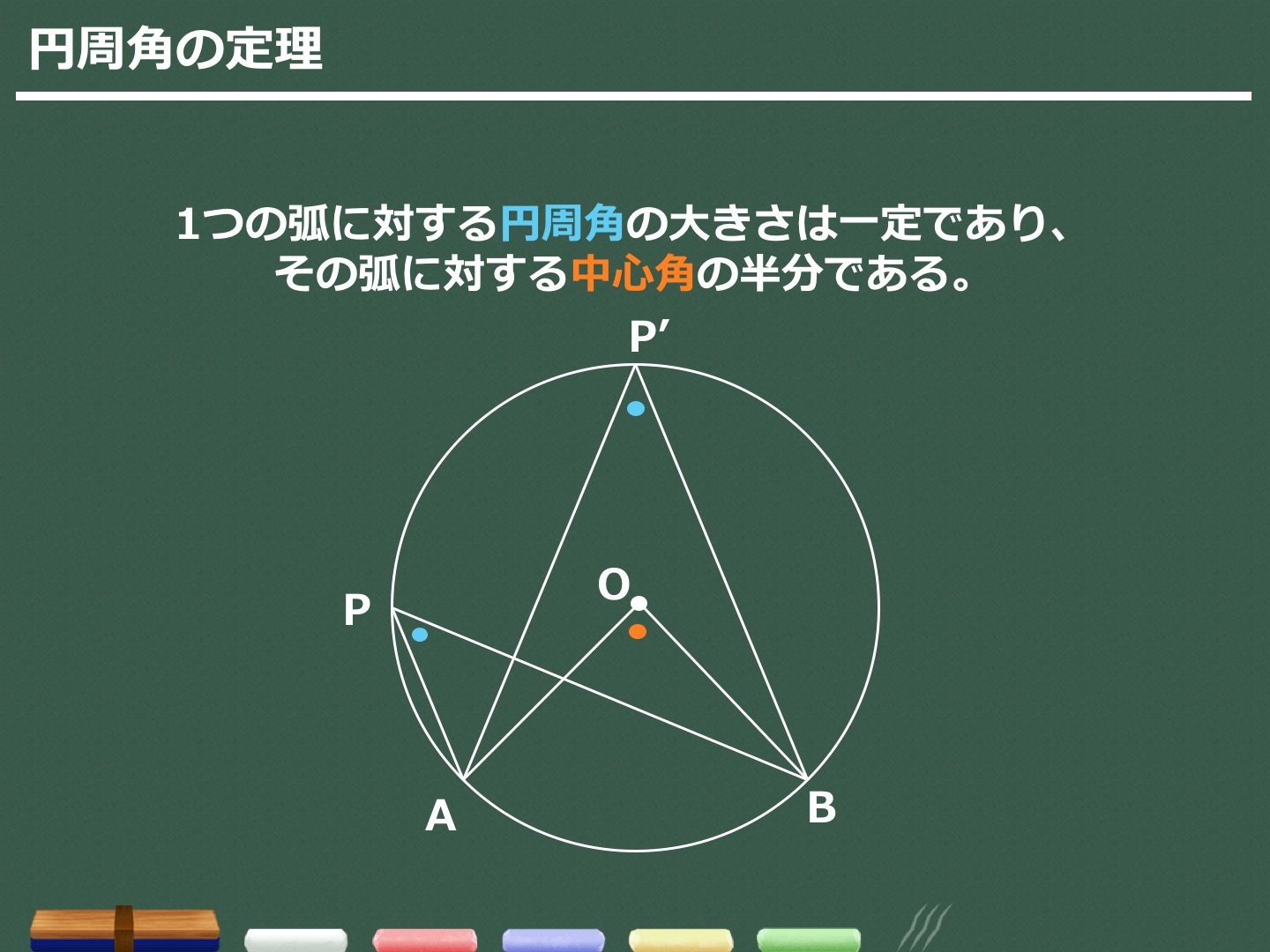 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 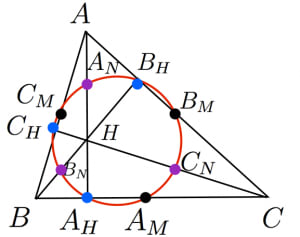 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |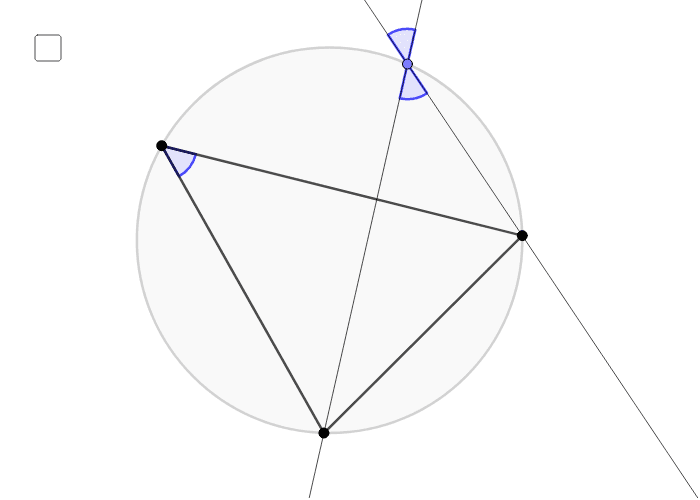
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  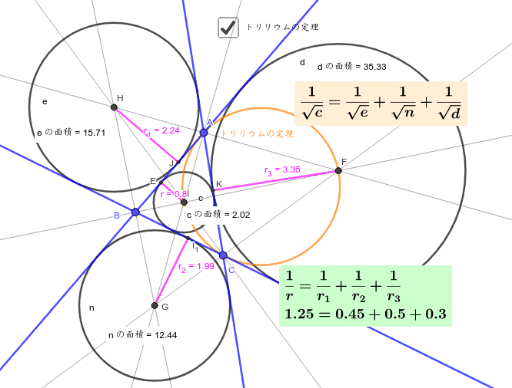円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 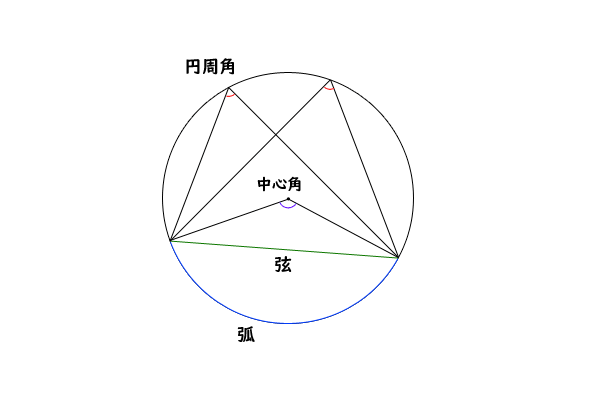 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 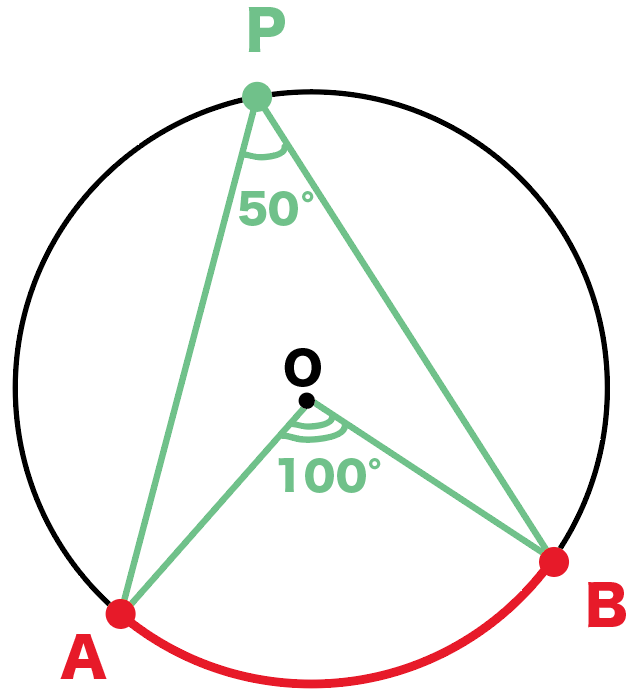 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 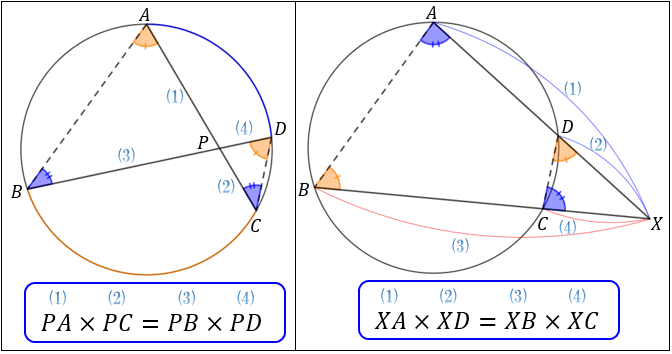 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
「円 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |  円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 | 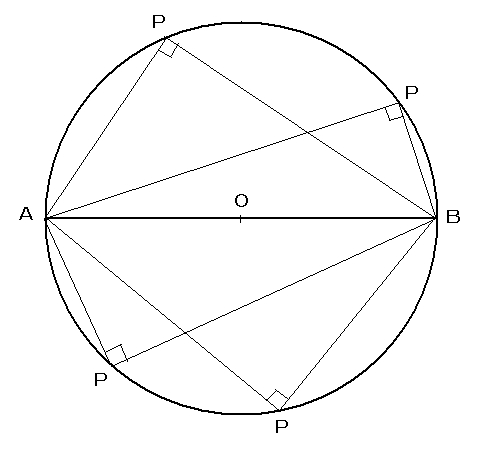 円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学 |
方べきの定理とは，円と点 P P P と2本の直線が作る図形において， P A 1 × P A 2 = P B 1 × P B 2 PA_1\times PA_2=PB_1\times PB_2 P A 1 × P A 2 = P B 1 × P B 2 が成立するという定理です。方べきの定理は全部で3パターンあります。 「円の接線 \(at\) と弦 \(ab\) が作る角 \(∠bat\) は、弦 \(ab\) に対する円周角 \(∠acb\) と等しい」という定理を、接弦定理と言います。 接弦定理は、\(∠bat\) が鋭角・直角・鈍角のどの場合でも成り立ちますが、それぞれ証明の仕方が少しずつ変わってきます。
0 件のコメント:
コメントを投稿